Der folgende Artikel ist am 2. Februar 2021 in der Medienwoche erschienen.
Seit Beginn der Corona-Pandemie hangeln sich gewisse Medienschaffende, Politikerinnen und auch Wissenschaftler mit Hilfe von Statistiken in halsbrecherischem Tempo von spekulativen Behauptungen über Scheinkorrelationen zu kausalen Schnellschüssen. Ein gutes Beispiel dafür ist die Diskussion um den Nutzen von Masken zur Eindämmung von Corona [0]. Zuerst schliessen einige voreilig auf deren Wirksamkeit, bloss weil in Ländern mit wenigen Covid-19-Fällen auch Gesichtsmasken verbreitet sind. Dann behaupten andere fälschlicherweise, dass Masken nichts nützen würden, weil auch in Ländern mit Maskenpflicht die Infektionszahlen nach oben schnellen. Kein Wunder also, dass Statistikerinnen und datenaffine Forschende mit Korrekturen, Kontextualisierungen und Kassandrarufen kaum mehr nachkommen [1] [2].
Neu ist der Missbrauch von Statistiken aber ebenso wenig wie die Haltung, dass ihnen deswegen nicht zu trauen sei. Schon Mark Twain vermerkte 1907 in seiner Autobiografie, es gebe «nur drei Arten von Lügen: Lügen, verdammte Lügen und Statistiken» [3]. Auch der eingangs zitierte Satz stammt wohl aus der ersten Hälfte des vergangenen Jahrhunderts und wird gemeinhin Winston Churchill zugeschrieben – ironischerweise gibt es dafür nicht den geringsten Beleg. Sicher ist bloss, dass Statistiken schon lange misstrauisch beäugt werden, weil man mit ihnen vortrefflich lügen und täuschen kann.
Anstatt das Missbrauchspotential von statistischen Informationen und Analysen zum Anlass zu nehmen, besonders vorsichtig damit umzugehen, scheinen viele den umgekehrten Weg zu gehen: Wenn sich mit Statistiken alles und sein Gegenteil beweisen lässt, dann folgt daraus schliesslich Beliebiges. Wieso also nicht selber zur Fälscherin oder zum Lügner werden? Dabei steckt hinter statistischem Unfug häufig nicht einmal eine böse Absicht. «Hanlons Rasiermesser» reicht in der Regel als Erklärung: «Schreibe nicht der Böswilligkeit zu, was durch Gedankenlosigkeit erklärbar ist» [4].
Zu dieser Gedankenlosigkeit gehört, Statistik wahlweise als methodischen Jekami-Werkzeugkasten oder als Massenware zu betrachten, ohne die dazugehörigen theoretischen und empirischen Voraussetzungen zu berücksichtigen. Ausdruck davon sind die vielen zweifelhaften Berechnungen und Statistiken zu Corona, die in den sozialen Netzwerken, aber auch in etablierten Medien von statistischen Laien mit grossem Selbstbewusstsein erstellt, interpretiert und verbreitet werden [5]. Vor allem zu Beginn der Pandemie wurde damit eine vermeintliche Gewissheit über den Zustand der Welt simuliert, die sich bei genauer Betrachtung in Luft auflöste.
Nur langsam wurde in der medialen Berichterstattung beispielsweise dem Umstand Rechnung getragen, dass die offiziellen Fallzahlen mit Unsicherheiten behaftet waren und dass es selbst beim Erheben der Todeszahlen grosse nationale Unterschiede gab [6]. So flossen die Corona-Todesfälle in italienischen und britischen Pflegeheimen anfangs nicht systematisch in die veröffentlichten Statistiken ein [7], wohingegen Belgien von Beginn weg sogar Verdachtsfälle ohne labordiagnostischen Nachweis mitzählte [8]. Mit den offiziellen Statistiken konnte man den epidemiologischen Verlauf gar nicht exakt und in Echtzeit abbilden, sondern lediglich eine zeitverzögerte Annäherung daran wagen. Auch hierzulande hätte das spätestens dann klar werden müssen, als die Probleme bei der Datenerfassung beim Bundesamt für Gesundheit BAG aufgezeigt wurden [9].
Die Diagramme und Statistiken von täglich oder sogar stündlich aktualisierten und bis auf den einzelnen Fall genau angegebenen Corona-Zahlen in den Medien schufen jedoch eine ganz andere, diskursive Wirklichkeit: Eine Wirklichkeit, in der man in jedem Land und zu jedem Zeitpunkt über jeden einzelnen Corona-Fall genau Bescheid wusste. Daran ändern auch relativierende Fussnoten oder kleingedruckte Erklärungen wenig, sodass publizierte Corona-Zahlen immer wieder implizit mit der Zahl der tatsächlich infizierten Menschen gleichgesetzt wurden und werden.
Statistiken schaffen ihre eigenen Wirklichkeiten
Auch bei anderen Fragen wird die statistische Annäherung an ein physikalisches, biologisches oder soziales Phänomen gerne gleichgesetzt mit dem Phänomen selbst – zum Beispiel, wenn die Neue Zürcher Zeitung titelt: «Ende 2018 lebten 8’544’527 Einwohner in der Schweiz» [10]. In der Tat ist das die Zahl, die das Bundesamt für Statistik BfS für die ständige Wohnbevölkerung im Jahr 2018 angibt [11]. In dieser Genauigkeit ist das aber schon deshalb falsch, weil beispielsweise die Zahl der vielen Sans-Papiers darin nicht enthalten ist [12].
Das dürfte die naive Vorstellung hoffentlich erschüttern, dass solche Bevölkerungsstatistiken die Wirklichkeit abbilden würden. Vielmehr schaffen sie eine Wirklichkeit, indem sie ohne Kontext als Referenzpunkt für wissenschaftliche Untersuchungen, öffentliche Diskussionen oder politische Entscheidungen dienen – zum Beispiel, um den Ausländeranteil in der Schweiz zu schätzen oder das Schweizer Pro-Kopf-Einkommen zu berechnen.
Das heisst freilich nicht, dass die Bevölkerungszahlen des BfS frei erfunden, unnütz oder notwendigerweise irreführend wären. Für viele praktische Anwendungen ist die Kenntnis der exakten Einwohnerzahl ja kaum relevant. Ob man bei der Berechnung des Pro-Kopf-Einkommens von 2018 [13] gerundete 8.544 Millionen oder exakt 8’544’527 Einwohner als Grundlage verwendet, macht einen Unterschied von fünf Franken oder 0.06 Promille – so oder so hatte die Schweiz mit gut 84’000 Schweizer Franken weltweit eines der höchsten Bruttoinlandprodukte pro Kopf.
Aus den Unsicherheiten in einer bestimmten Hinsicht die Abwesenheit von Gewissheiten in jeder anderen Hinsicht abzuleiten, ist also fehlschlüssiger Unsinn [14]. Trotzdem geschieht das erschreckend häufig. So versuchen einige Menschen zum Beispiel, die Gefahr von Covid-19 mit den oben erwähnten Unsicherheiten in den Statistiken kleinzureden: Schliesslich wisse man ja nicht einmal, ob die Menschen «an» oder «mit» Corona gestorben seien [15]. Insinuiert wird damit, dass die vielen Toten des vergangenen Jahrs nichts Aussergewöhnliches seien, weil die Menschen ohnehin bald gestorben wären.
Nun gibt es tatsächlich Fälle [16], in denen die Infektion mit dem Virus nichts mit dem Tod der Infizierten zu tun hat. Das sagt jedoch nichts darüber aus, wie stark solche Fälle statistisch überhaupt ins Gewicht fallen, und warum zurzeit so viele Menschen zusätzlich sterben [17]. Aus dem plötzlichen Tod derart vieler Menschen eine fatalistische Normalität zu basteln, erinnert an die argumentativen Verrenkungen des Universalgelehrten Pangloss in Voltaires Satire Candide. Auch Pangloss theoretisiert die schlimmsten individuellen und kollektiven Schicksalsschläge mit Scheinargumenten weg. Für ihn können die Dinge gar nicht anders sein, als sie sind, weil sie sich angeblich bereits im besten aller möglichen Zustände befänden. So ist dann auch ein Erdbeben, das 30’000 Todesopfer fordert, für Pangloss «nichts Neues» und damit auch kein Grund, aus der Ruhe zu geraten [18]. Bei Corona scheinen das einige ähnlich zu sehen: Schliesslich seien früher auch schon Menschen an der Grippe gestorben, betroffen seien laut Statistik ohnehin nur «alte» und «immunschwache» Menschen und das Sterben gehöre nun einmal zum Leben dazu.
Auch das ist eine Form, mit Statistiken alternative diskursive Wirklichkeiten zu schaffen und damit abertausende von Einzelschicksalen darunter zu begraben. Wer nur noch über (unsichere) Statistiken redet, rückt das individuelle Sterben so weit in den Hintergrund, dass es seinen Schrecken verliert. Das funktioniert mit Corona-Opfern so gut wie mit Terror-Toten [19] oder mit Menschen, die an Tuberkulose, AIDS oder Malaria sterben [20]. Schliesslich ist der Tod eines einzigen Menschen eine Katastrophe, hunderttausend Tote aber blosse Statistik, wie schon 1925 der Journalist und Satiriker Kurt Tucholsky geschrieben hat [21].
Dass Statistiken eigene Wirklichkeiten schaffen, ist indes keine neue Einsicht [22]. Sie geht nur regelmässig vergessen. Die Folge ist ein verhängnisvoller Datenfetischismus, der eine statistische Annäherung an eine Wirklichkeit mit einer detailgetreuen Abbildung von der Wirklichkeit gleichsetzt. Im Umkehrschluss führt das dazu, dass all das, was statistisch nicht erfasst ist, aufhört zu existieren – zumindest im öffentlichen Diskurs. Im Sommer machte das Schweizer Fernsehen SRF beispielsweise Schlagzeilen mit der Behauptung, dass «zwei von drei Covid-19-Ansteckungen im Ausgang» stattfinden würden [23]. Kurz darauf stellte sich heraus, dass diese Aussage auf einem Eingabefehler beruhte – neu war laut SRF das familiäre Umfeld der häufigste Ansteckungsort [24]. Zutreffend war jedoch weder die erste noch die zweite Behauptung.
Wer die publizierten Zahlen des SRF (793 Meldungen zwischen dem 16. Juli und dem 1. August, davon 320 mit fehlenden Angaben oder unbekanntem Ansteckungsort [23]) ins Verhältnis setzt zu den im gleichen Zeitraum offiziell gemeldeten Fallzahlen (2138, [25]) und deren Ansteckungsort, kommt nämlich zu einem ganz anderen Schluss: In über drei Vierteln dieser Fälle (1665) war unbekannt, wo sich die Menschen ansteckten. Weder im Bericht des SRF noch in den darauffolgenden politischen Diskussionen spielten diese unbekannten Ansteckungsorte jedoch eine wesentliche Rolle: Viele Debattenteilnehmer schienen sich mit den bekannten Orten zu begnügen und schafften die grossmehrheitlich unbekannten Ansteckungsorte damit diskursiv aus der Welt.
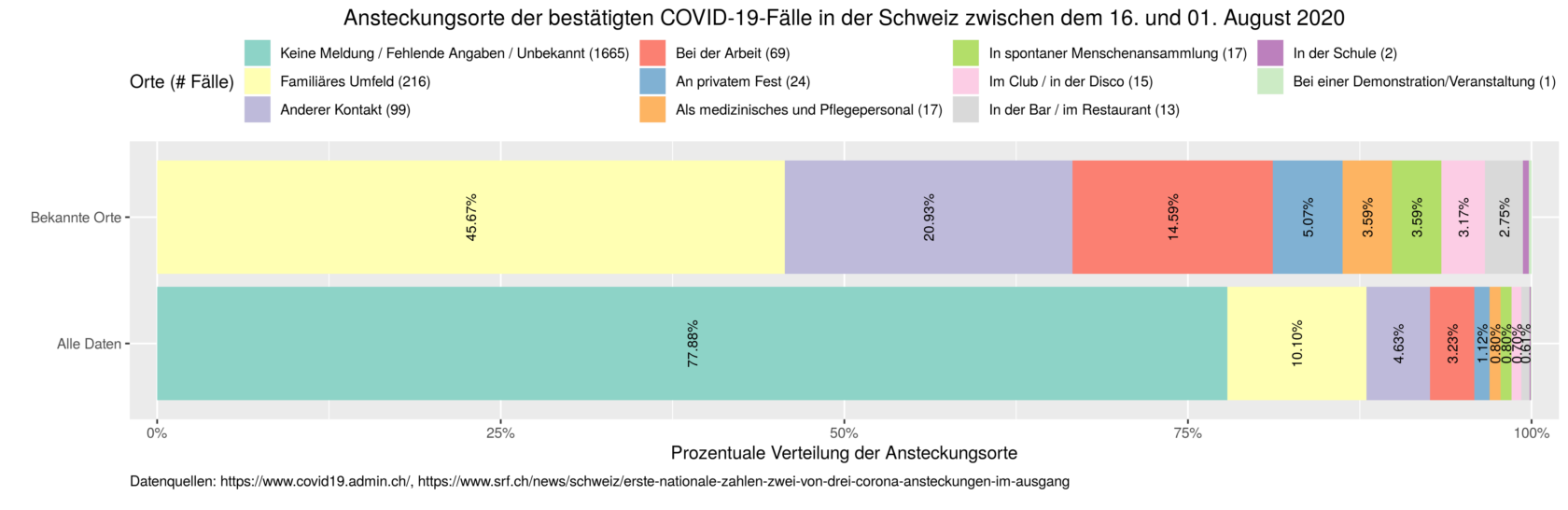
Ob die unbekannten Ansteckungsorte weggelassen werden, macht in diesem Fall einen gewaltigen Unterschied in der Beurteilung.
Wie die Statistik zu einem mächtigen «sozialen Trick» wird
Auch in der Wissenschaft schaffen Statistiken Wirklichkeiten, die es sonst nicht gäbe. So hängt es zwar in erster Linie von biologischen, chemischen und mitunter auch psychischen und sozialen Faktoren ab, ob ein bestimmtes Medikament therapeutisch wirkt. Ob diese Wirksamkeit aber von Forschenden erkannt und vor allem, ob sie von den Zulassungsbehörden anerkannt wird, unterliegt fast immer statistischen Regeln. Denn die wissenschaftlichen Ergebnisse, welche die therapeutische Wirksamkeit angeblich aufzeigen, könnten auch andere Ursachen haben als die Inhaltstoffe des Medikaments: Dahinter könnte beispielsweise der Placebo-Effekt stecken oder es könnte sich um ein Zufallsergebnis handeln, das bei der Wiederholung des Versuchs verschwindet. Die Statistik gibt Regeln vor, wie sich diese alternativen Erklärungen zwar nicht vollständig ausschliessen, aber zumindest probabilistisch eingrenzen lassen.
In diesem Zusammenhang erfüllen statistische Methoden nicht nur eine wissenschaftliche, sondern auch eine soziale Rolle, indem sie die Legitimationsgrundlage schaffen für die Zulassung und Anwendung des Medikaments. Weil die wenigsten von uns die statistischen Kompetenzen besitzen, um diese Legitimationsgrundlage fachlich nachvollziehen zu können, wird die Statistik damit zu einem mächtigen «sozialen Trick» (frei nach dem Sozialarbeiter Stefan M. Seydel [26]): Mit ihrer Hilfe wird ein potentiell wirksames Medikament vor den Augen von Krankenkassen, Ärztinnen und Patienten in ein anerkannt wirksames Medikament verwandelt. An den biologischen oder chemischen Eigenschaften des Medikaments ändert das freilich nicht das Geringste – sie tragen vor der statistischen Beurteilung genauso viel oder wenig zur therapeutischen Wirksamkeit bei wie nachher. Was sich aber verändert, ist unser Vertrauen darin, dass diese Eigenschaften einen therapeutischen Effekt haben.
Daran ist nichts Verwerfliches und selbstverständlich ist die Statistik nicht alleine an diesem Trick beteiligt. Die soziale Funktion der Statistik tut auch ihrer wissenschaftlichen Verlässlichkeit keinen Abbruch. Sie bedeutet lediglich, dass statistische Ergebnisse Vertrauen schaffen können, ohne dass die Vertrauenden diese Ergebnisse bis ins Detail nachvollziehen müssen. Wir vertrauen dem Trick, weil er – richtig angewendet – zu einigermassen verlässlichen Ergebnissen führt, um therapeutisch wirksame Medikament zu erkennen und anzuerkennen. Wir erhalten damit Medikamente, die gegen eine bestimmte Krankheit im Durchschnitt besser wirken als ein Placebo oder ein bereits bekanntes Arzneimittel.
Werden Statistiken jedoch ausschliesslich als Tricks eingesetzt, also losgelöst von ihren vielen Annahmen und Voraussetzungen, wird es schnell irreführend (siehe Box 1). So wird aus einem berechtigten sozialen Trick der täuschende Trick eines Taschenspielers, der seinem Publikum jene statistische Sorgsamkeit bloss vorgaukelt, die den Trick wissenschaftlich und sozial überhaupt erst legitimieren würde.
Gerade in gesellschaftspolitischen Debatten laufen statistische Taschenspieler zur Hochform auf: Wenn Zahlen angeblich «für sich sprechen» [27] oder «jemandem Recht geben» [28], steckt dahinter nicht selten der Versuch, einer bestimmten politischen Haltung ohne weitere Begründung objektive Geltung zu verschaffen. Damit
wird der Blick verstellt auf die vielen beschreibenden, erklärenden oder normativen Annahmen, die der Erhebung, Auswertung und Interpretation dieser Daten zugrunde liegen. Diese Annahmen können besser oder schlechter empirisch gestützt oder theoretisch begründet sein, aber es bleiben dennoch Annahmen, die sich nicht aus den Daten selbst ergeben, sondern «von aussen» hinzukommen. Wer Zahlen sprechen hört, sollte deshalb zum Arzt gehen – die Statistikerin kann beim besten Willen nicht mehr helfen.
Box 1: Statistischer Unfug in den Wissenschaften
Statistiken werden auch in datengetriebenen Wissenschaften wie der Biologie oder der Medizin regelmässig falsch oder missbräuchlich eingesetzt. Ein Beispiel dafür ist der Missbrauch des sogenannten «p-Werts», der in vielen wissenschaftlichen Studien eine entscheidende Rolle beim Einordnen der Ergebnisse spielt.
Stark vereinfacht ausgedrückt beschreibt der p-Wert, wie überraschend ein beobachtetes Resultat basierend auf bestimmten Annahmen über die Welt ist: Je kleiner der Wert, desto überraschender das Resultat [1]. Wer beispielsweise eine nicht manipulierte Münze zehnmal wirft, der erwartet im Durchschnitt fünfmal Kopf und fünfmal Zahl. Wer nun aber wider Erwarten nur zweimal «Kopf» oder «Zahl» erhält, braucht nicht besonders stutzig zu werden: Der p-Wert für ein solches Resultat beträgt knapp 0.11: In 11 Prozent der Fälle sind bei zehn Würfen einer Münze zwei oder weniger Mal «Kopf» oder «Zahl» zu erwarten. Sollte bei zehn Münzwürfen aber kein einziges Mal «Zahl» oder kein einziges Mal «Kopf» oben liegen, ist das viel überraschender. Der p-Wert liegt dann unter 0.002: So ein Ergebnis ist in weniger als 2 Promille der Fälle zu erwarten, wenn die Münze nicht manipuliert ist. Es wäre falsch daraus zu schliessen, dass etwas faul ist, aber es könnte sich lohnen, noch einmal zehn Würfe anzuhängen, um der Sache auf den Grund zu gehen.
Für sich genommen sagt der p-Wert nichts über die Qualität oder die Bedeutung eines wissenschaftlichen Resultats aus. Trotzdem ist er im vergangenen Jahrhundert in vielen biologischen und medizinischen Disziplinen zum unbarmherzigen Richter darüber aufgestiegen, ob wissenschaftliche Ergebnisse als «relevant» anerkannt werden: Ist der p-Wert klein genug, halten viele einen Effekt fälschlicherweise für «bewiesen». Ist er zu gross, schliessen viele – ebenso falsch – auf die Abwesenheit eines Effekts. Damit wird einem einzelnen statistischen Mass eine Bedeutung zugewiesen, das dieses in vielen Fällen gar nicht verdient. Forschende werden dadurch dazu verleitet, der statistischen Analyse etwas «nachzuhelfen» um einen möglichst tiefen p-Wert zu erhalten. «p-Hacking» nennt sich dieser Missbrauch von Statistik, mit der tote Lachse denken lernen und die aus Schokolade ein Diätprodukt macht [2].
Der Taschenspieltrick ist dabei im Prinzip immer der gleiche: Man bearbeitet die Daten so, dass der p-Wert unter einen vordefinierten Schwellenwert fällt. Dann tut man so, als sei dadurch hinreichend gezeigt, dass am beschriebenen Effekt etwas dran ist – ganz egal, wie klein der Effekt tatsächlich ist oder wie sehr er bisherigen Ergebnissen und Theorien widerspricht. Dass der Trick aufgeht, liegt primär daran, dass vielen Forschenden fälschlicherweise beigebracht wird, dass ein kleiner, also statistisch signifikanter p-Wert gleichbedeutend ist mit einem wissenschaftlich signifikanten Resultat – ganz unabhängig von den experimentellen Voraussetzungen.
Referenzen Box 1:
[1] Die obigen Resultate beruhen auf der Annahme, dass die Wahrscheinlichkeit von «Kopf» und «Zahl» jeweils 50 Prozent beträgt bei einer nicht manipulierten Münze. Korrekt ist das nur in der Theorie. Tatsächlich ist bei Münzwürfen jene Seite mit grösserer Wahrscheinlichkeit oben, welche beim Beginn des Wurfs oben liegt – der Unterschied ist mit 51 Prozent zu 49 Prozent aber so klein, dass es mehrere hunderttausend Münzwürfe bräuchte, um ihn statistisch einigermassen überzeugend nachzuweisen. Siehe dazu «Persi Diaconis et al. (2007). Dynamical Bias in the Coin Toss. SIAM Review (https://statweb.stanford.edu/~cgates/PERSI/papers/dyn_coin_07.pdf, abgerufen am 09. Januar 2020).)
[2] Servan Grüninger (25.03.2016). Der P(roblem)-Wert. NZZ (https://www.nzz.ch/karriere/studentenleben/der-problem-wert-ld.133818, abgerufen am 04. Januar 2020).
Statistiken sind reich an Voraussetzungen
Dass die Erhebung von Daten an zahlreiche Voraussetzungen geknüpft ist, hat die Diskussion über die Sicherheiten und Unsicherheiten von Corona-Fallzahlen gezeigt. Darüber hinaus braucht es aber auch Annahmen, um Daten sinnvoll beschreiben und interpretieren zu können. Schon für das einfache Problem, zwei Punkte im zweidimensionalen Raum zu verbinden, lassen sich unendlich viele mathematische Lösungen finden: Eine Gerade kommt dafür ebenso in Frage wie eine Funktion, die eine Kurve oder eine Welle beschreibt. Welche soll man nun wählen? Das hängt vom Kontext der Daten und der konkreten Fragestellung ab. Eine Schallwelle mit einer Geraden beschreiben zu wollen, wäre Unsinn. Ebenso unsinnig wäre es, etwas anderes als eine Gerade zu nehmen, um die Distanz zwischen zwei Gebäuden anzugeben.
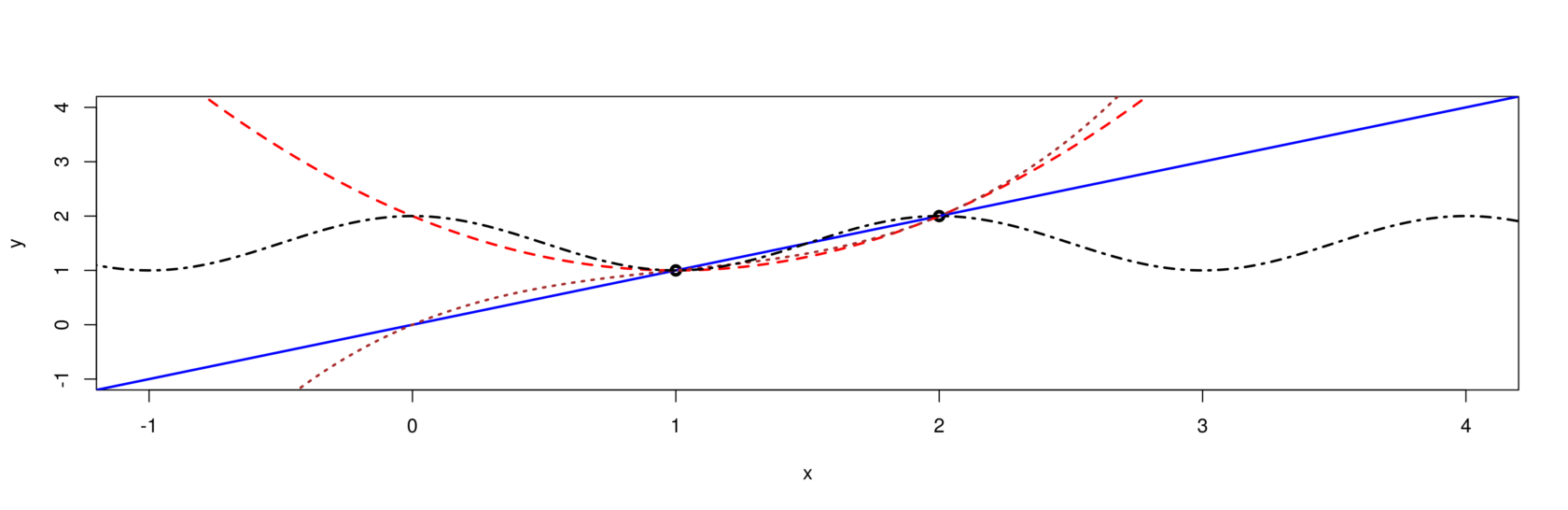
Es gibt unendlich viele Möglichkeiten, die beiden obigen Punkte zu verbinden. Die Wahl der «richtigen» Lösung hängt von Kriterien ab, die ausserhalb der Daten selbst liegen.
Auch die Frage, wie viel Geld der «typische» Schweizer auf der Seite hat, ist gar nicht so einfach beantwortet. Soll man das arithmetische Mittel (oft einfach «Durchschnitt» genannt), den Modus oder den Median verwenden, um die vorhandenen Vermögensdaten zusammenzufassen? Alle drei Statistiken geben «typische» Eigenschaften einer Datenmenge wieder, werden aber unterschiedlich berechnet (siehe dazu Box 2).
Die Wahl der Statistik beeinflusst direkt, wie hoch das «typische» Schweizer Vermögen ist, denn der Durchschnittsschweizer ist um einiges vermögender als der Modus- oder der Medianschweizer [29]. Auch hier lässt sich die Wahl der «richtigen» Statistik nicht allein mit Blick auf die Daten begründen, da sie im Wesentlichen davon abhängt, was man unter «typisch» versteht und woran man konkret interessiert ist. In allen drei Fällen werden nämlich Informationen vernichtet, welche für eine bestimmte Frage irrelevant, für eine andere Frage aber entscheidend sein könnten.
Manchmal kann es sogar sinnvoll sein, Daten gar nicht erst zusammenzufassen, sondern die Informationen auf eine andere Art und Weise «wegzuwerfen»: Wenn das Schauspielhaus für ein Theaterstück versehentlich auf dem Plakat den «Pfauen», aber auf der Website den «Schiffbau» angibt, dann wäre es absurd, diese beiden Daten zusammenzufassen und anzunehmen, die Aufführung würde auf halbem Weg dazwischen, also mitten auf den Gleisen des Zürcher Hauptbahnhofs, stattfinden. Sinnvoller ist es, sich zufällig für eine der beiden Adressen zu entscheiden (oder einfach das Telefon zur Hand zu nehmen, um die Veranstalter anzurufen) [30].
Wenn schon derart simple Beispiele vor Voraussetzungsreichtum strotzen, sollte man sich in weniger überschaubaren Situationen umso mehr hüten, Daten und Statistiken gedankenlos eine Bedeutung zuzuweisen, die sie womöglich gar nicht haben. Das ist insbesondere dann der Fall, wenn man darauf gestützt kausale Zusammenhänge aufstellt oder normative Forderungen stellt. Ob man beispielsweise bei grösserer Unsicherheit in der Datengrundlage mit mehr oder weniger Vorsicht handeln soll, können Daten für sich genommen nicht sagen.
Box 2: Wie beschreibende Statistiken Informationen vernichten
Beschreibende Statistiken fassen Daten auf eine bestimmte Weise zusammen. Um den «typischen» Wert einer Datenmenge zu berechnen, lässt sich beispielsweise das arithmetische Mittel (auch «Durchschnitt» genannt), der Modus oder der Median verwenden, die jeweils unterschiedlich berechnet werden.
Der Durchschnitt bezeichnet die Summe aller Werte geteilt durch die Zahl der Beobachtungen, mit dem Modus ist der häufigste Wert gemeint und der Median entspricht derjenigen Zahl, welche die vorhandenen Werte so unterteilt, dass die eine Hälfte darunter, die andere Hälfte darüber liegt.
Ein Beispiel: Eine Klasse aus 7 Schüler*innen schreibt eine Matheprüfung und erhält die folgenden Noten [1, 2, 3, 4, 5, 5, 6]. Die Durchschnittsnote liegt damit bei 3.7, der Median bei einer 4, der Modus bei einer 5.
Wie bei jeder Zusammenfassung gehen auch bei solchen Statistiken Informationen verloren. Das heisst, dass Durchschnitt, Modus und Median nur einen Teil der Informationen wiedergeben, die sich in der ganzen Datenmenge finden lässt. Wer weiss, dass die Median-Note des Mathe-Tests bei einer 4 liegt, hat damit noch keine Informationen darüber, wie sich die Noten auf die einzelnen Schüler*innen verteilen. Die Noten können so verteilt sein wie oben beschrieben. Eine Median-Note von 4 ergibt sich aber auch, wenn alle Schüler*innen eine 4 schreiben, d.h. [4, 4, 4, 4, 4, 4, 4] (Fall 1), oder wenn drei Schüler*innen eine 1, drei eine 6 und jemand eine 4 schreiben, d.h. [1, 1, 1, 4, 6, 6, 6] (Fall 2). Um das Leistungsniveau der Klasse zu beurteilen, ist der Median damit nur bedingt nützlich: Im ersten Fall sind alle Schüler*innen auf dem gleichen Niveau, im zweiten Fall gibt es hingegen massive Unterschiede – der Median vernichtet diese zusätzlichen Informationen.
Allgemein formuliert heisst das, dass sich hinter dem gleichen Durchschnitts-, Modus- oder Medianwert ganz unterschiedliche Datenmengen verstecken können, wie die folgenden Grafiken beispielhaft zeigen. Die Daten der einzelnen Histogramme stammen aus sehr unterschiedlichen Wahrscheinlichkeitsverteilungen. Deren Durchschnittswerte (rot durchgezogene Linie) sind dabei überall gleich, aber die Mediane (grün gestrichelt) und Modi (violett gepunktet) können sich stark unterscheiden. Welche der drei Statistiken am sinnvollsten ist, um die Daten zusammenzufassen, lässt sich pauschal nicht beantworten, da es von der konkreten Fragestellung abhängt.
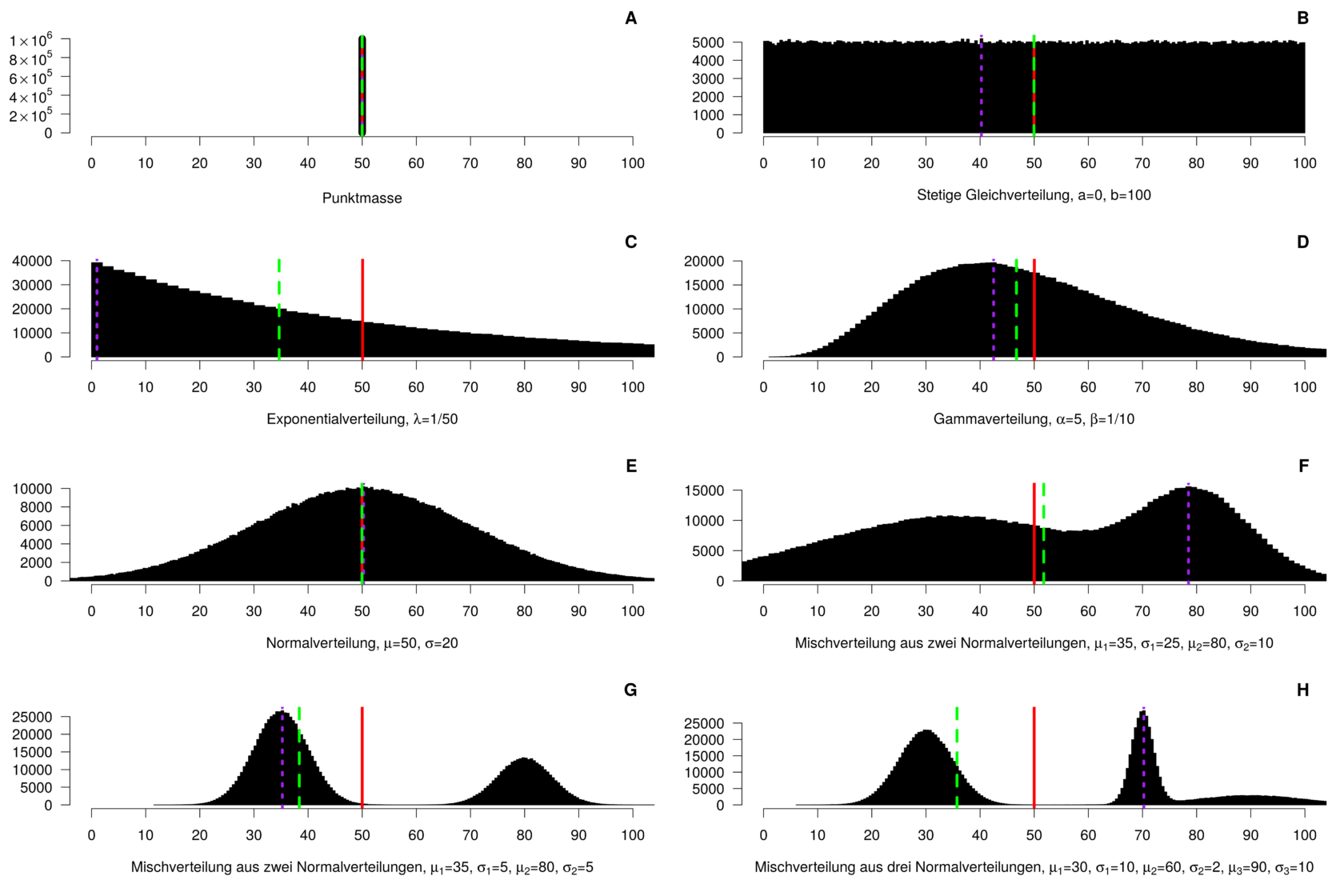
Von oben links nach unten rechts: A) Eine Punktmasse, bei der alle Werte exakt dem Durchschnitt entsprechen. B) Eine stetige Gleichverteilung, bei der alle Werte zwischen 0 und 100 gleich wahrscheinlich sind. Median und Durchschnitt fallen zusammen, der Modus entspricht zufällig einem der Balken. C) Eine Exponentialverteilung mit Skalenparameter 1/50; der Modus fällt auf den Balken mit dem tiefsten Wert, der Median liegt zwischen Modus und Durchschnitt. D) Eine
Gammaverteilung mit Formparameter 5 und Ratenparameter 1/10; der Median liegt zwischen Modus und Durchschnitt. E) Eine Normalverteilung mit Mittelwert 50 und Standardabweichung 20; Durchschnitt, Median und Modus fallen zusammen. F) Ein Mischung zweier Normalverteilungen; der Durchschnitt ist am tiefsten, der Modus am höchsten und der Median dazwischen. G) Eine andere Mischung zweier Normalverteilungen. Hier ist die Reihenfolge genau umgekehrt: Der Modus ist am tiefsten, der Median liegt dazwischen, der Durchschnitt ist am höchsten. H) Die Mischung von drei Normalverteilungen; hier liegt für der Durchschnitt in der Mitte
zwischen Median und Modus.
Die Corona-Pandemie als statistischer Anschauungsunterricht
Die Corona-Pandemie hat gezeigt, welchen Schaden der gedanken- und voraussetzungslose Umgang mit Daten in gesellschaftlichen Debatten und bei politischen Entscheiden anrichten kann. Das Problem liegt nicht in erster Linie darin, dass sich Fachfremde mit Statistik auseinandersetzen – im Gegenteil: Angesichts der grossen Bedeutung von statistischen Kennzahlen in gesellschaftspolitischen Debatten ist es begrüssenswert, wenn die Diskussion über Fallzahlen, Ansteckungswahrscheinlichkeiten und Tödlichkeitsraten zu einem gesteigerten Interesse an Statistik als wissenschaftliche Disziplin führt. Wenn Menschen einer statistisch unterfütterten Behauptung nicht einfach bereitwillig Glauben schenken, sondern sich zuerst einmal fragen, woher die Daten stammen, wie und in welchem Kontext sie erhoben worden sind und ob sie die Behauptung überhaupt stützen [5], dann ist schon viel erreicht, um den öffentlichen Umgang mit Statistiken redlicher zu gestalten.
Ein Problem besteht erst dann, wenn das Selbstvertrauen beim Erstellen oder Verwenden von Statistiken schneller wächst als die dafür notwendigen fachlichen Kompetenzen. Die Statistik wird dann schnell ein reines Mittel zum Zweck, um die Daten in die «gewünschte» Form zu pressen. Das sind keine guten Voraussetzungen, um ein Bewusstsein für die Feinheiten statistischer Erhebungen, Auswertungen und Interpretationen zu schaffen.
Die Folge sind übertrieben selbstbewusste Anwender statistischer Methoden, die auf fachliche Einwände von Statistikerinnen überaus sensibel oder abwehrend reagieren können. Der Biostatistiker Stephen Senn meinte dazu einmal ironisch, es sei erstaunlich, wie leicht Nicht-Statistiker Statistik meistern würden. Er selbst studiere sie seit über 40 Jahren und verstehe sie noch immer nicht [31].
Es braucht mehr Datenkompetenz, um mit Statistiken die Wahrheit zu sagen.
Vielleicht sorgt der eklatante Mangel an statistischer Kompetenz bei der politischen und auch medialen Einordnung von Corona-Daten aber doch noch für den nötigen politischen Druck, um Veränderungen anzustossen. Das hoffen zumindest die Initiantinnen und Initianten des «Appells für eine dringliche nationale Datenkompetenz-Kampagne» [32]. Ziel des Appells ist es, den «Grundpfeiler einer nationalen Datenkultur» zu schaffen und einen «verantwortungsbewussten, kritischen, ethischen und nachhaltigen Umgang mit Daten» sicherstellen zu können (siehe dazu auch Box 3 unten).
Angesichts der enormen Defizite in der Datenkompetenz, welche die Corona-Pandemie in Medien, Politik und auch in Teilen der Wissenschaften offenbart, ist eine solche Kampagne dringend nötig. Andernfalls besteht die Gefahr, dass es zu einem Zustand ständiger Infodemie kommt, in dem Daten nur noch als beliebige und voraussetzungslose rhetorische Manövriermasse verwendet werden, um im politischen Seilziehen die Oberhand zu gewinnen [33].
Gerade weil statistische Informationen einen enormen Einfluss auf politische Entscheide haben, ist die Verbesserung der Datenkompetenz kein blosser Luxus, sondern eine notwendige Voraussetzung, um die informierte Mitsprache der Bürgerinnen und Bürger an solchen Entscheiden zu gewährleisten und einen redlichen öffentlichen Diskurs zu fördern. Vielleicht würden dann auch die Zyniker merken, dass man mit Statistiken zwar vortrefflich lügen kann, es aber auch ziemlich schwierig ist, ohne sie die Wahrheit zu sagen [34].
Box 3: Datenkompetenz verlangt mehr als einen Computer im Schulzimmer
In den Wissenschaften haben viele das Problem mangelnder Statistikkenntnisse erkannt und sich dazu verschrieben, die methodische Qualität in der Forschung systematisch zu analysieren und verbessern. Mittlerweise gibt es dafür sogar eigene Forschungseinrichtungen wie «METRICS» («Meta-Research Innovation Center at Standford») an der Universität in Stanford [35], das «QUEST»-Center («Quality, Ethics, Open Science, Translation») an der Berliner Charité [36] oder das «CRS» («Center for Reproducible Science») an der Universität Zürich [37]. Diese Einrichtungen «erforschen die Forschung» – sie untersuchen, wie verlässlich und aussagekräftig wissenschaftliche Methoden tatsächlich sind und wie sie sich verbessern lassen. Weil die Statistik in vielen wissenschaftlichen Disziplinen methodisch grundlegend ist, spielt die Verbesserung der statistischen Kompetenz unter Forschenden dabei eine wesentliche Rolle.
In der Politik braucht es wohl noch ein bisschen mehr Überzeugungsarbeit, bis die Bedeutung solcher Kompetenzen verstanden wird. Der Walliser CVP-Ständerat Beat Rieder hat jüngst eine Interpellation eingereicht, in der er eine nationale Datenkompetenz-Kampagne fordert [38]. Die Antwort des Bundesrats darauf spricht Bände: Mit einem Verweis auf die «Zuständigkeit der Kantone» und der Erwähnung bestehender Digitalisierungs-Programme ist das Thema für ihn erledigt. Mit der Förderung von «Digitalisierung» scheint er nämlich auch die Förderung von «Datenkompetenz» abgedeckt zu sehen – eine fatale Verkürzung, die auch Rieder kritisiert [39]: «Lesen und Schreiben lernt man [...] nicht dadurch, dass man [...] einen PC zur Verfügung gestellt erhält. Genauso wenig lernt man [daraus] Datenkompetenz.»
Referenzen
Servan Grüninger (15.11.2020). Twitter-Post (https://twitter.com/Sgruninger/status/1327990715205423104, abgerufen am 01. Februar 2021).
Servan Grüninger (12.03.2020). Coronavirus in den Medien: Von Experten und «Experten». Medienwoche (https://medienwoche.ch/2020/03/12/coronavirus-in-den-medien-von-experten-und-experten/, abgerufen am 04. Januar 2020).
Servan Grüninger (27.10.2020). Wissenschaft als Kassandra: «Wir haben es doch vorausgesagt!». Medienwoche (https://medienwoche.ch/2020/10/27/wissenschaft-als-kassandra-wir-haben-es-doch-vorausgesagt/, abgerufen am 04. Januar 2021).
Mark Twain (04.01.1907). Chapters from my Autobiography IX. North American Review. Seite 471 (https://www.gutenberg.org/files/19987/19987-h/19987-h.htm#CHAPTERS_FROM_MY_AUTOBIOGRAPHY_IX, abgerufen am 04. Januar 2021). Twain schreibt das Zitat dem britischen Politiker Benjamin Disraeli zu, aber die Ursprünge des Spruchs sind verworren. Siehe zum Beispiel «Peter M. Lee (19.07.2012). Lies, Damned Lies and Statistics. Persönlicher Blog (https://www.york.ac.uk/depts/m..., abgerufen am 06. Januar 2021)».
Effectiviology (n/a). Hanlon’s Razor: Why You Shouldn’t Start By Assuming the Worst (https://effectiviology.com/hanlons-razor/, abgerufen am 04. Januar 2021). Hanlon sprach von «Dummheit» (en. «stupidity») statt von «Gedankenlosigkeit», doch da auch intelligente Menschen mit ihren Einschätzungen katastrophal falsch liegen können, habe ich das Zitat leicht abgewandelt. Sinngemäss wurde die Aussage ohnehin schon viel länger verwendet – zum Beispiel in Goethes «Werther»: «Und ich habe, mein Lieber, wieder bei diesem kleinen Geschäft gefunden, dass Missverständnisse und Trägheit vielleicht mehr Irrungen in der Welt machen als List und Bosheit. Wenigstens sind die beiden Letzteren gewiss seltener.» Siehe «Johann Wolfgang von Goethe (1774). Die Leiden des jungen Werther. Erstes Buch: Am 4. Mai 1771 (https://www.projekt-gutenberg...., abgerufen am 08. Januar 2021)». Damit ist «Hanlons Rasiermesser» ein weiteres Beispiel, welches das ironische «Gesetz der Eponyme» des Statistikers Stephen Stiglers bestätigt, wonach keine wissenschaftliche Entdeckung nach ihrem ursprünglichen Entdecker benannt ist.
Servan Grüninger (15.05.2020). Corona-Statistiken auf dem Prüfstand: Was uns Schweizer Medien servieren. Medienwoche (https://medienwoche.ch/2020/05/15/corona-statistiken-auf-dem-pruefstand-was-uns-schweizer-medien-servieren/, abgerufen am 04. Januar 2021).
Marie-José Kolly (04.05.2020). Wie die Corona-Welle Länder unterschiedlich erfasst (und woran das liegen könnte). Republik (https://www.republik.ch/2020/05/04/wie-die-corona-welle-verschiedene-laender-erfasst-und-woran-das-liegen-koennte, abgerufen am 04. Januar 2021).
Servan Grüninger (30.03.2020). Covid-19-Statistiken: Worauf musst Du achten? – Teil 2. Persönlicher Blog (https://www.servangrueninger.ch/blogcomplete/covid-19-statistiken-worauf-musst-du-achten-teil-2, abgerufen am 04. Januar 2021).
Daniel Steinvorth (20.10.2020). «Regeln sind immer für die anderen». NZZ (https://www.nzz.ch/international/interview-belgien-corona-regeln-sind-immer-fuer-die-andern-ld.1582502, abgerufen am 04. Januar 2021).
Adrienne Fichter (20.03.2020). «Die Zahl der Todesfälle haben wir aus Wikipedia entnommen». Republik (https://www.republik.ch/2020/03/20/die-zahl-der-todesfaelle-haben-wir-aus-wikipedia-entnommen, abgerufen am 04. Januar 2021).
SDA (29.11.2019). Ende 2018 lebten 8’544’527 Einwohner in der Schweiz – ein Viertel waren Ausländer. NZZ (https://www.nzz.ch/schweiz/ende-2018-lebten-8544527-einwohner-in-der-schweiz-ein-viertel-waren-auslaender-ld.1525336, abgerufen am 04. Januar 2021).
Bundesamt für Statistik (29.09.2020). Bevölkerungsdaten im Zeitvergleich, 1950-2019 (https://www.bfs.admin.ch/bfs/de/home/statistiken/bevoelkerung.assetdetail.14367961.html, abgerufen am 04. Januar 2021).
Didier Ruedin (02.03.2018). Wie viele «Sans-Papiers» gibt es überhaupt in der Schweiz? NCCR «on the move» (https://blog.nccr-onthemove.ch/wie-viele-sans-papiers-gibt-es-uberhaupt-in-der-schweiz/, abgerufen am 04. Januar 2021).
Bundesamt für Statistik (28.09.2020). Bruttoinlandprodukt nach Verwendungsarten (https://www.bfs.admin.ch/bfs/de/home/statistiken/volkswirtschaft/volkswirtschaftliche-gesamtrechnung/bruttoinlandprodukt.assetdetail.14347458.html, abgerufen am 04. Januar 2021).
Daniel-Pascal Zorn (07.01.2016). Na logisch! Der mereologische Fehlschluss. Hohe Luft (https://www.hoheluft-magazin.de/2016/01/na-logisch-der-mereologische-fehlschluss/, abgerufen am 04. Januar 2021).
SRF News Plus / Thomas Häusler (03.12.2020). Sterben die Menschen mit oder an Corona? SRF (https://www.srf.ch/news/schweiz/tuecken-bei-todeszahlen-sterben-die-menschen-mit-oder-an-corona, abgerufen am 04. Januar 2021).
Bettina Zanni (01.01.2020). Kanton Zürich schliesst Covid als Todesursache von 29-Jährigem aus. 20 Minuten (https://www.20min.ch/story/bag-meldet-tod-eines-buben-und-eines-jungen-erwachsenen-957494160533, abgerufen am 04. Januar 2021).
Euromomo (2021). Z-scores by country (https://www.euromomo.eu/graphs-and-maps#z-scores-by-country, abgerufen am 04. Januar 2021).
Ein gutes Beispiel dafür liefert Pangloss’ Reaktion auf das Erdbeben von Lissabon. Als er und Candide in Lissabon ankommen, bricht ein fürchterliches Erdbeben aus, das 30’000 Menschen unter den Trümmern begräbt unt tötet. Auch Candide wird dabei verletzt und bittet seinen Lehrer – des Sterbens nahe auf der Strasse liegend – um ein bisschen Wein. Statt seinem Schützling zu helfen, erwidert Pangloss bloss, dass solche Erdbeben nichts Neues seien. Im amerikanischen Lima habe vor einigen Jahren auch schon die Erde gebebt: Gleiche Ursachen, gleiche Wirkung. Er sei sicher, dass es eine unterirdische Schwefelschicht zwischen Lissabon und Lima gebe. Erst als Candide das Bewusstsein verliert, bemüht sich er darum, ihm zu helfen. Mit seiner schulmeisterlich vorgetragenen Erklärung vermittelt Pangloss den Eindruck, als sei an den 30’000 Toten und an der Verletzung seines Schützlings nichts Schlimmes zu finden, weil es ja «nichts Neues» sei und solche Erdbeben eben zum Leben dazugehören würden. Laut Pangloss können die Dinge gar nicht anders sein, als sie sind, da sie bereits im besten aller möglichen Zustände seien. Er begründet das zwar mit der Vorsehung Gottes, was heute wohl nicht mehr so viele Menschen überzeugen dürfte. An die Stelle Gottes sind mit «der Natur» oder «dem Schicksal» aber andere Mächte getreten, die in der Diskussion um Corona beschworen werden, um die Toten wegtheoretisieren zu können: Schliesslich seien früher ja auch schon Menschen an Infektionskrankheiten gestorben – das Sterben gehöre halt dazu zum Leben. Siehe «Voltaire (1759). Candide ou l’optimisme. Kapitel 5 (http://www.gutenberg.org/cache/epub/4650/pg4650.html, abgerufen am 08. Januar 2021)».
Servan Grüninger (13.09.2016). Zahlenterror mit Terrorzahlen. NZZ (https://www.nzz.ch/karriere/studentenleben/wahrscheinlichkeit-zahlenterror-mit-terrorzahlen-ld.135634, abgerufen am 04. Januar 2021).
Servan Grüninger (30.08.2020). Ebola tötet – Tuberkulose auch. NZZ Campus (https://www.servangrueninger.ch/blogcomplete/ebola-ttet-tuberkulose-auch, abgerufen am 04. Januar 2021).
Garson O’Toole (21. Mai 2010). A Single Death Is a Tragedy; A Million Deaths Is a Statistic. Quote Investigator (https://quoteinvestigator.com/2010/05/21/death-statistic/). Tucholsky gab damit die Aussage eines französischen Diplomaten wieder: «Der Krieg? Ich kann das nicht so schrecklich finden! Der Tod eines Menschen: das ist eine Katastrophe. Hunderttausend Tote: das ist eine Statistik!»
Alain Desrosières (2001). How Real Are Statistics? Four Possible Attitudes. Social Research (https://www.jstor.org/stable/40971461?seq=1, abgerufen am 04. Januar 2021).
Servan Grüninger (01.08.2020). Twitter-Post. Twitter (https://twitter.com/SGruninger/status/1289529486321434627, abgerufen am 04. Januar 2021).
SRF/SDA/SCHP (02.08.2020). BAG korrigiert: Meiste Ansteckungen in Familie, nicht in Clubs. SRF (https://www.srf.ch/news/schweiz/corona-uebertragungen-bag-korrigiert-meiste-ansteckungen-in-familie-nicht-in-clubs).
Bundesamt für Gesundheit (04.01.2021). COVID-19 Switzerland. Information on the current situation, as of 4 January 2021 (https://www.covid19.admin.ch/en/overview?ovTime=total, abgerufen am 04. Janaur 2021).
SMS2SMS (25.09.2020). Twitter-Post. Twitter (https://twitter.com/sms2sms/status/1309420696624402432, abgerufen am 04. Januar 2021).
Servan Grüninger (16.03.2020). Auch bei Covid-19 gilt: Zahlen sprechen nie für sich. Higgs (https://www.higgs.ch/auch-bei-covid-19-gilt-zahlen-sprechen-nie-fuer-sich/30114/, abgerufen am 06. Januar 2021).
Servan Grüninger (10.09.2020). Statistiken geben niemandem recht, können aber Rechthaber entlarven. Reatch (https://reatch.ch/publikationen/statistiken-geben-niemandem-recht-koennen-aber-rechthaber-entlarven, abgerufen am 06. Januar 2021).
Servan Grüninger (21.07.2015). Weg mit Durchschnittsschweizer! NZZ Campus (https://www.servangrueninger.ch/blogcomplete/weg-mit-dem-durchschnittschweizer, abgerufen am 04. Januar 2021).
Das Beispiel ist inspiriert von «John Venn (1878). The Foundations of Chance. The Princeton Review. Seite 497 (https://quod.lib.umich.edu/m/moajrnl/acf4325.3-01.002/501:19?page=root;rgn=full+text;size=100;view=image, abgerufen am 06. Januar 2021)». Die Originalbeispiel lautet sinngemäss: Der Kapitän eines Kriegschiffs bereitet sich darauf vor, eine gegnerische Festung einzunehmen, und schickt zwei Spione los, um die Grösse der vom Gegner verwendeten Kanonenkugeln in Erfahrung zu bringen. Diese Information braucht er, um nach der Eroberung der Festung genügend Kugeln dabei zu haben, um sie verteidigen zu können. Das Problem: Ein Spion berichtet, dass die Kugeln einen Durchmesser von 8 Zoll haben, der andere sagt hingegen, es seien 9 Zoll. Würde der Kapitän das arithmetische Mittel der beiden Angaben verwendetn (8.5 Zoll), hätte er garantiert die falschen Kugeln dabei. Besser ist es deshalb, sich zufällig für eine der beiden Angaben zu entscheiden (oder, wenn möglich, Kugeln beider Grössen einzupacken).
Stephen Senn (27. November 2014). Twitter-Post. Twitter (https://twitter.com/stephensenn/status/538017638111531009, abgerufen am 04. Januar 2021).
Data Literacy:Appell für eine dringliche nationale Datenkompetenz-Kampagne (https://www.data-literacy.ch/, abgerufen am 04. Januar 2021).
Servan Grüninger (2020.03.10). Statistiken sollten Erkenntnisse schaffen, nicht Meinungen bestätigen. NZZ (https://www.nzz.ch/meinung/statistiken-sollten-erkenntnisse-schaffen-nicht-meinungen-bestaetigen-ld.1540276, abgerufen am 04. Januar 2021).
Der Satz ist inspiriert von einem ähnlich lautenden Zitat («Es ist einfach, mit Statistik zu lügen. Es ist schwierig, ohne sie die Wahrheit zu sagen»), das gemeinhin dem schwedischen Mathematiker Andrejs Dunkels zugeschrieben wird. Einen Originalnachweis konnte ich dafür aber leider nicht finden.
BIH Quest Center for Transforming Biomedical Research (https://www.bihealth.org/en/research/quest-center, abgerufen am 04. Januar 2020).
Center for Reproducible Science (https://www.crs.uzh.ch/en.html, abgerufen am 04. Januar 2020).
Beat Rieder (2020.09.24). Nationale Datenkompetenzkampagne. Datenkompetenz (Data Literacy) ist gefragt. Interpellation an den Bundesrat. Geschäft 20.4173 Das Schweizer Parlament (https://www.parlament.ch/de/ra..., abgerufen am 04. Januar 2020).
[5] Beat Rieder (2020.12.17). Diskussion des Geschäfts 20.4173 im Ständerat. Das Schweizer Parlament (https://www.parlament.ch/de/ratsbetrieb/amtliches-bulletin/amtliches-bulletin-die-verhandlungen?SubjectId=51467, abgerufen am 04. Januar 2020).
Die Beiträge auf dem Reatch-Blog geben die persönliche Meinung der Autor*innen wieder und entsprechen nicht zwingend derjenigen von Reatch oder seiner Mitglieder.



Comments (0)