Datenanalyse zwischen Daten und Deutung: Mit Statistik neue Erkenntnisse schaffen

Eine sorgfältige Datenanalyse beginnt stets mit einer akribischen Fehlerkontrolle und -bereinigung. Zudem ist es oft notwendig, Variablen zu transformieren (Recodierung) oder gar neu zu konstruieren (Indizes), sofern es der Datensatz erfordert. Es ist von zentraler Bedeutung, die spezifische Natur des vorliegenden Datensatzes zu verstehen, da nur so die adäquate Analysemethode ausgewählt werden kann.

Zu den ersten Schritten zählt dabei oft die Betrachtung von sogenannten «Lagemasse» wie dem Median oder Mittelwert, gefolgt von Streuungsmassen wie der Standardabweichung oder dem Interquartilsabstand. Diese statistischen Kennzahlen verschaffen einen ersten Eindruck vom Charakter der Daten. Weiterführend bieten grafische Darstellungen wie Histogramme oder Balkendiagramme nicht nur eine visuelle Perspektive, sondern erleichtern auch die anschließende Entscheidung hinsichtlich der geeignetsten Analysemethode (vgl. Abbildung 1). Eine visuelle Betrachtung der Daten ist grundsätzlich immer zu empfehlen, denn sie schützt vor voreiligen Annahmen und verhindert, dass man unbedacht zu fehlerhaften Analyseergebnissen gelangt.

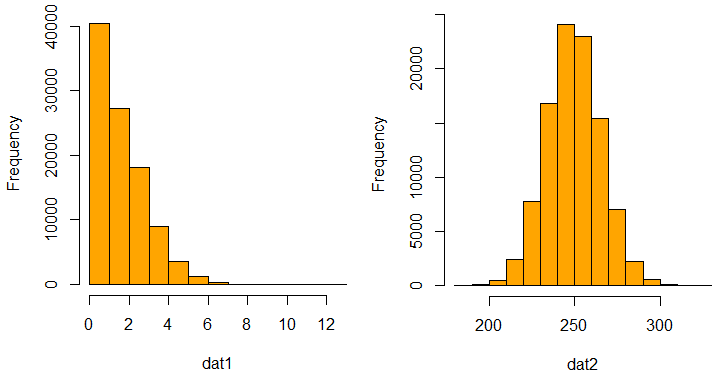
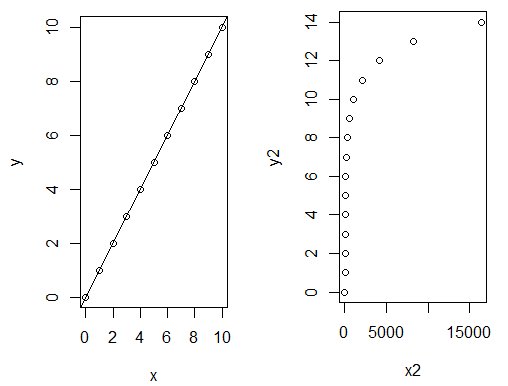
Je nach Datenverteilung (siehe Abbildung 1) und Beziehung zwischen zwei (oder mehr) Merkmalen und der Beziehungsart (siehe Abbildung 2) kann es nun sein, dass zum Beispiel eine lineare oder logistische Regression am besten zur Analyse der Daten geeignet ist.

Weiterhin ist auch Fachwissen nötig, um einschätzen zu können, ob die Daten plausibel sind oder ob beispielsweise schon eine systematische Verzerrung enthalten ist. Beispielsweise wäre eine Stichprobe, die nur aus Kleinwüchsigen besteht, keine repräsentative Stichprobe für die gesamte Bevölkerung. Und eine Umfrage nur unter den Studierenden einer Universität zu ihrem Essverhalten ist auch kaum repräsentativ für die gesamte Bevölkerung.

Es gibt zwei grundlegend verschiedene Arten, wie Daten analysiert werden können: Die deskriptive bzw. beschreibende Statistik zielt, wie der Name sagt, auf eine möglichst genaue Beschreibung von Daten ab. Demgegenüber steht die schliessende bzw. inferentielle Statistik, welche Daten dazu verwendet, um allgemeine Schlüsse zu ziehen, welche über den einzelnen Datensatz hinausgehen. Obwohl beide Ansätze dazu dienen, Informationen aus Daten zu extrahieren, haben sie unterschiedliche Ziele und Vorgehensweisen (siehe Abbildung 3).

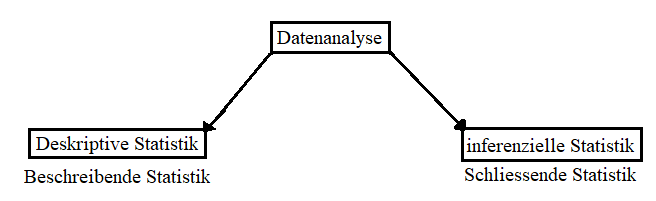
Beschreibende Statistik

Die beschreibende Statistik nutzt statistische Mittel, um Beschreibungen der Stichprobe vorzunehmen. Sie dient vor allem dazu, Daten zu beschreiben, zu visualisieren und durch Tabellen und Grafiken zusammenzufassen, um so die Hauptmerkmale der Daten hervorzuheben. Dazu werden unter anderem Kennzahlen für die Häufigkeit der Werte, Lage der Daten sowie Verteilungsbreite verwendet.

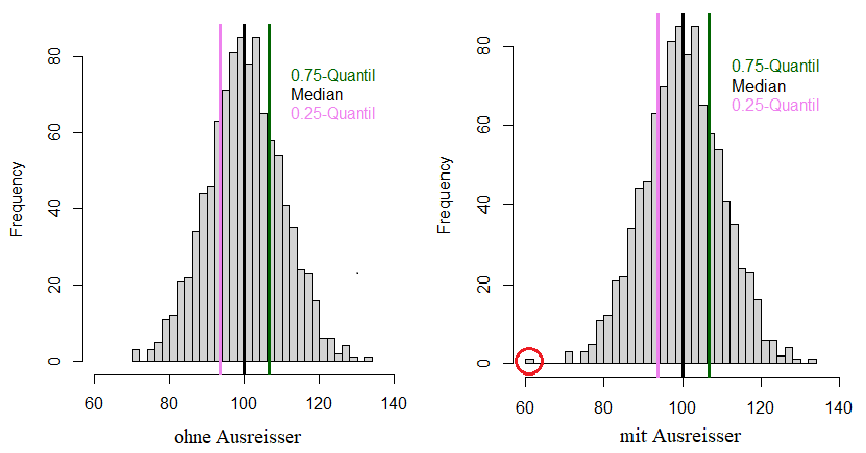
Das arithmetisches Mittel, auch Mittelwert oder Durchschnitt genannt, ist ein Lagemass und wird berechnet, indem die Summe aller Werte in einer gegebenen Datenmenge durch die Anzahl der Werte geteilt wird. Der Mittelwert ist vergleichsweise anfällig auf Ausreisser (siehe Abbildung 4). Ein klassisches Beispiel dafür ist die Vermögensverteilung: Wenn 9 von 10 Personen keinerlei Vermögen haben, die zehnte jedoch 10 Millionen Schweizer Franken besitzt, sind im Durchschnitt alle Millionäre.

Der Median ist ebenfalls ein Lagemass und gibt die «Mitte» der Datenverteilung an, indem er die Daten in zwei gleich grosse Hälften teilt. Die Werte in einer Hälfte der Daten sind grösser bzw. gleich, die Werte der anderen Hälfte kleiner bzw. gleich dem Median. Im obigen Beispiel mit der Vermögensverteilung liegt der Medianwert bei 0 Schweizer Franken.

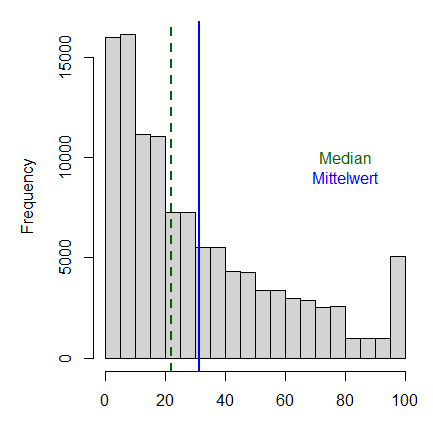
Ein weiteres Lagemass ist der Modus, auch Modalwert genannt. Damit wird jener Wert in den Daten bezeichnet, der am häufigsten vorkommt. Im obigen Beispiel wäre das wiederum 0 CHF, in Abbildung 4 ist der Modus mit dem zweiten Balken von links dargestellt.

Unter den Streuungsmassen gehört die Standardabweichung gemeinsam mit der Varianz zweifellos zu den bedeutendsten. Die Standardabweichung ist die Quadratwurzel der Varianz und gibt an, wie stark die einzelnen Datenpunkte durchschnittlich um den Erwartungswert der Daten streuen (siehe Abbildung 5).

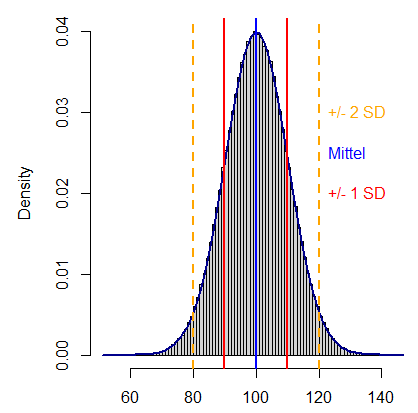
Die Spannweite, ein weiteres Streuungsmass, gibt die Differenz zwischen dem grössten und dem kleinsten Beobachtungswert an. Weil die Spannweite somit auf den beiden extremsten Werten basiert, reagiert sie besonders empfindlich auf Ausreisser. Robuster gegenüber Ausreissern ist hingegen der Quartilsabstand, also die Differenz zwischen dem obersten und dem untersten Viertel der Datenpunkte (siehe Abbildung 6). Der Quartilsabstand verändert sich bei einer Änderung der grössten oder kleinsten Werte (im Gegensatz zur Spannweite) des Datensatzes in der Regel nicht, da diese Werte zur Berechnung nicht herangezogen werden.

Ziel der beschreibenden Statistik ist es somit, die Daten zu charakterisieren und ihre wichtigsten Eigenschaften zu identifizieren. Ausserdem werden komplexe Daten in eine verständliche und leicht interpretierbare Information umgewandelt.

Schliessende Statistik

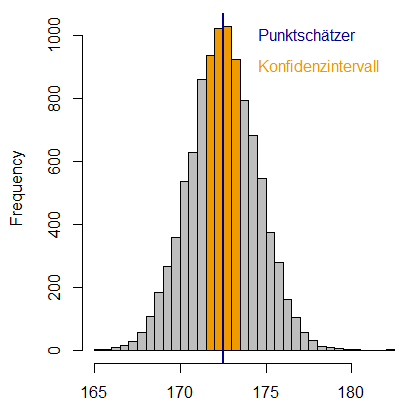
Während die beschreibende Statistik bei der genauen Beschreibung von Daten Halt macht, versucht die schliessende Statistik aus einer Stichprobe Rückschlüsse zu ziehen über Eigenschaften der gesamten Population, aus der die Stichprobe stammt. Ein Beispiel ist die Ermittlung der durchschnittlichen Haltbarkeit (Verfallsdatum) von Lebensmittelprodukten. Hierbei ist es wie bei den Körpergrössen nicht praktikabel, alle hergestellten Produkte bis zu ihrem tatsächlichen Verfallsdatum zu überwachen, da dies viel Zeit und Ressourcen erfordern würde. Stattdessen wird eine Stichprobe der Produkte vorgenommen und anhand von Ergebnissen aus dieser Stichprobe Schlussfolgerungen über die Haltbarkeit aller hergestellten Produkte gezogen. Die schliessende Statistik verwendet dazu verschiedene Schätzmethoden und Hypothesentests, welche meist Lage- oder Streuungsmasse vergleichen. So versucht eine sogenannte Punktschätzung einen einzelnen Schätzwert oder Punkt zu berechnen, der als beste Schätzung für einen unbekannten Parameter in einer Population oder einem Datensatz dient. Ein häufig verwendeter Punktschätzer ist das arithmetische Mittel einer Stichprobe, um den Erwartungswert in der gesamten Population zu schätzen. Versucht man beispielsweise, die durchschnittliche Körpergrösse der Schweizer Bevölkerung zu erfassen, könnte man zufällig eine Stichprobe von 1000 Menschen in der Schweiz auswählen, deren Körpergrösse erfassen und dann basierend darauf den Durchschnitt berechnen. Dieser Durchschnitt entspräche dann nicht genau dem Durchschnitt aller in der Schweiz wohnhaften Menschen, aber er würde als Punktschätzer eine verlässliche Annäherung daran bieten (siehe Abbildung 7).

Da jeder Punktschätzer mit Unsicherheiten behaftet ist, gibt es auch sogenannte Intervallschätzung, bei denen nicht nur ein einzelner Punkt als Schätzwert für einen unbekannten Parameter (z.B. die Durchschnittskörpergrösse) in einer Population angegeben wird, sondern ein Intervall von Werten (siehe Abbildung 7). Das Konfidenzintervall ist ein solcher Intervallschätzer. Es gibt einen Bereich an, in dem man den gesuchten Parameter vermutet, sowie eine Wahrscheinlichkeit, die angibt, wie häufig man im Durchschnitt mit dieser Vermutung richtig liegt. So gibt das 95%-Konfidenzintervall an, dass in 95 von 100 Fällen der wahre Wert in diesem Intervall liegt. Wenn man also 100 Mal ein 95%-Konfidenzintervall für die Durchschnittskörpergrösse berechnet, dann würden durchschnittlich 95 dieser 100 Konfidenzintervalle den wahren Parameterwert der durchschnittlichen Körpergrösse in der Bevölkerung enthalten. Das Konfidenzintervall enthält den wahren Wert oder nicht und darf nicht mit dem Kredibilitätsintervall verwechselt werden, welches angibt, mit welcher Wahrscheinlichkeit der wahre Parameterwert im Intervall liegt. Der Zweck der Intervallschätzung besteht darin, Unsicherheiten in der Schätzung eines Parameters zu berücksichtigen.

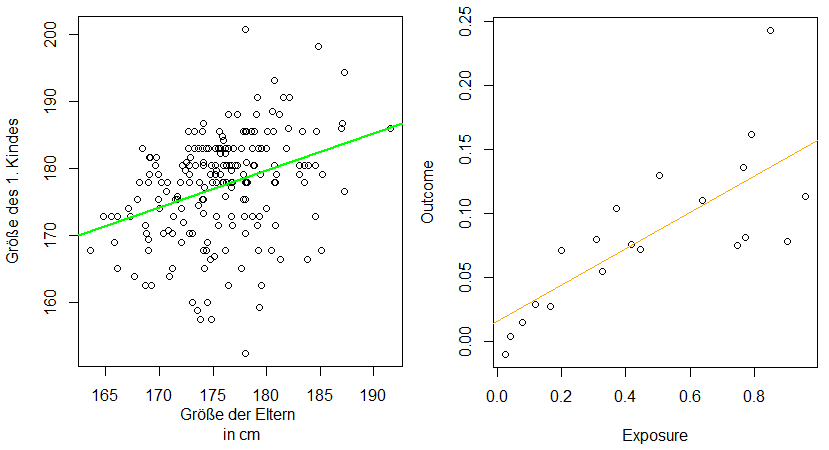
Wenn es darum geht, den Zusammenhang zwischen einer abhängigen Variablen und einer oder mehreren unabhängigen Variablen zu untersuchen, greifen Forschende oft zur linearen Regression (siehe Abbildung 8). Sie ist besonders nützlich, um Vorhersagen zu treffen, Trends zu analysieren, die Intensität von Beziehungen zwischen Variablen zu beurteilen oder untypische Werte zu identifizieren. Mit ihrer Hilfe kann beispielsweise die Beziehung zwischen dem Einkommen einer Person und ihrem Bildungsstand modelliert werden, um zukünftige Einkommensentwicklungen vorherzusagen.

Oft werden Schätz- oder Regressionsmethoden zusammen mit sogenannten Hypothesentests verwendet. Anders als Verfahren, die auf die Quantifizierung unbekannter Parameter abzielen, dient der Hypothesentest der Überprüfung spezifischer Annahmen oder Hypothesen bezüglich einer Grundgesamtheit, und zwar auf Basis von Stichprobenergebnissen. In der Essenz wird mittels Stichproben untersucht, ob eine bestimmte behauptete Annahme für eine Population statistisch haltbar ist oder nicht.

Die schliessende Statistik ist unerlässlich, um auf Basis von Stichprobendaten allgemeingültige Rückschlüsse auf eine Gesamtpopulation zu treffen. Sie findet Anwendung in zahlreichen Fachbereichen – von der Naturwissenschaft über die Wirtschaft bis hin zu den Sozialwissenschaften – und liefert dort essenzielle Grundlagen für fundierte Entscheidungsprozesse und wissenschaftliche Erkenntnisgewinnung.

In der praktischen Anwendung sind deskriptive und schliessende Statistik häufig miteinander verflochten. Während die deskriptive Statistik eine erste Analyse und Darstellung der vorliegenden Daten leistet, knüpft die schliessende Statistik daran an und zieht generalisierbare Schlüsse für die untersuchte Gesamtpopulation. Beide zusammen liefern ein ganzheitliches Bild des untersuchten Phänomens und bilden so die Basis für umfassende Datenauswertungen.

Jede statistische Analyse muss mit sogenannten Zufallsfehlern, auch als «random error» bezeichnet, umgehen können. Der Zufallsfehler beschreibt all jene kleinen oder grossen Fluktuationen, welche die Daten oder die Datenerhebung beeinflussen und zu einer Streuung der Resultate führen. Wer beispielsweise zufällig die Körpergrösse von 100 Menschen in der Schweiz vermisst, wird jedes Mal ein leicht anderes Ergebnis erhalten, wobei jedoch alle Ergebnisse zufällig um die tatsächliche durchschnittliche Körpergrösse in der Schweiz streut. Diese Streuung bezeichnet man als Zufallsfehler. Er beeinflusst die Präzision eines Ergebnisses, also die Nähe wiederholter Messungen aneinander.

Ein Bias, auch Verzerrung genannt, stellt demgegenüber einen vermeidbaren, systematischen Fehler in wissenschaftlichen Untersuchungen dar. Er tritt auf, wenn Ergebnisse nicht mehr den tatsächlichen Gegebenheiten entsprechen und somit von der eigentlichen Wahrheit abweichen (sogenannte Richtigkeit oder «trueness» im Englischen). Solche systematischen Abweichungen können beispielsweise durch systematische Messfehler, Auswahlverzerrungen oder Informationsverzerrungen entstehen. Wer zum Beispiel die durchschnittliche Körpergrösse in der Schweiz messen möchte, aber bei der Stichprobenauswahl nur Männer berücksichtigt, wird eine nach oben verzerrte Schätzung erhalten, weil Männer im Durchschnitt grösser sind als Frauen. Ein anderer systematischer Fehler würde auftreten, wenn man zur Messung ein Metalllineal nutzt, das bei 20°C kalibriert wurde, die Messung aber bei einer Raumtemperatur von 12°C vornimmt. Die Messergebnisse werden systematisch etwas zu gross ausfallen, da sich das Metall etwas zusammenzieht und somit die Kalibrierung nicht mehr stimmt.

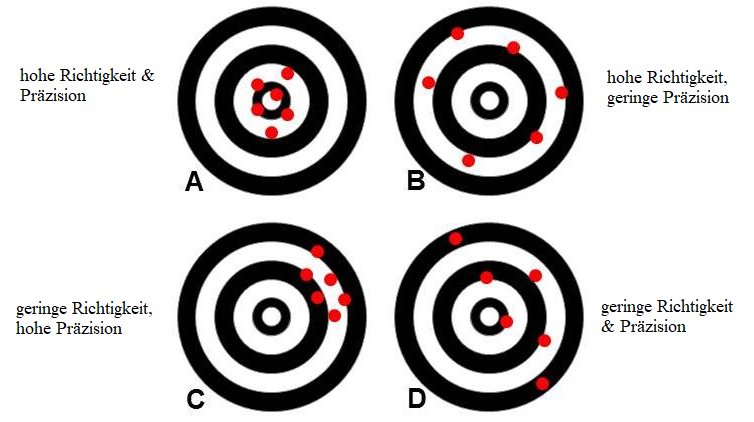
Das Ziel in wissenschaftlichen Untersuchungen ist es, sowohl den Bias als auch den Zufallsfehler zu minimieren, um verlässliche und genaue Resultate zu erhalten (siehe Abbildung 9). Zufallsfehler lassen sich reduzieren, indem man die Stichprobengrösse erhöht, sodass die statistischen Schätzer genauer werden. Systematische Verzerrungen sind zumeist schwieriger zu beheben, da nicht immer klar ist, woher sie stammen. Es gibt jedoch verschiedene statistische Methoden, um ihren Einfluss zu reduzieren. So sorgt eine zufällige Auswahl von Stichproben bzw. im Falle von experimentellen Erhebungen die zufällige Zuteilungen zu den einzelnen experimentellen Gruppen dafür, dass systematische Verzerrungen eliminiert werden. Würden Forschende beispielsweise bei einem Medikamententest keine randomisierte und verblindete Zuteilung der Teilnehmenden in Kontroll- und Testgruppe vornehmen, sondern alle Teilnehmenden basierend auf ihren Vorerkrankungen in eine der beiden Gruppen zuteilen, wäre das Ergebnis schon allein wegen dieser Zuteilung verzerrt. Würden beispielsweise bei einer Krebsstudie alle Patienten mit grossen Tumoren in die Kontrollgruppe und alle Patienten in die Testgruppe eingeteilt, würde die Testgruppe am Ende der Studie wohl die besseren Krankheitsverläufe vorweisen. Doch aufgrund der verzerrten Zuteilung wäre nicht klar, ob das auf das verabreichte Medikament oder auf die unterschiedlichen Tumorgrössen oder beides zurückzuführen ist. Eine zufällige Zuteilung ist auch deshalb wichtig, um unbekannte Verzerrungen zu minimieren (siehe Abbildung 10).

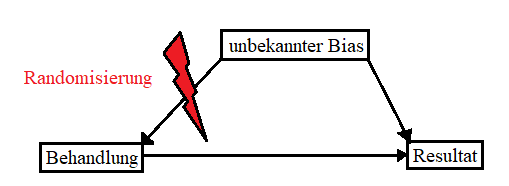
Ohne Randomisierung hätte nämlich dieser unbekannte Faktor sowohl auf das Resultat als auch auf die Behandlung eine Auswirkung, sodass nicht festgestellt werden kann, ob die Veränderung im Resultat vom Bias oder der Behandlung kommt.

Im gleichen Masse kann Verblindung dabei helfen, systematische Fehler zu verhindern. Beispielsweise führt eine ungleiche Behandlung von Kontroll- und Testgruppe zu einem systematischen Performance-Bias und eine ungleichmässige Aufteilung der Versuchsteilnehmenden in beiden Gruppen zu einem Selektionsbias. Neben diesen drei Fehlertypen gibt es noch weitere systematische Fehler, sodass eine gute statistische Studienplanung essentiell ist, um Biases in Studien zu minimieren.

Die Bedeutung der Statistik in der wissenschaftlichen Forschung kann nicht hoch genug eingeschätzt werden. Sie dient nicht nur der Beschreibung und Interpretation von Daten, sondern auch der Überprüfung wissenschaftlicher Hypothesen. In diesem Kontext ermöglicht die statistische Datenanalyse eine tiefergehende Auseinandersetzung mit empirisch gewonnenen Daten und lässt Erkenntnisse zu, die sonst im Datenwust verborgen bleiben würden.

Durch den Einsatz statistischer Verfahren können komplexe Datenmengen vereinfacht, Muster und Zusammenhänge erkannt sowie signifikante Ergebnisse von zufälligen Variationen unterschieden werden. Dies bildet die Basis, um fundierte wissenschaftliche Aussagen zu treffen und Hypothesen zu überprüfen.

Jedoch birgt die Anwendung statistischer Methoden auch Fallstricke. Systematische Fehler, auch als Bias oder Verzerrung bezeichnet, können die Ergebnisse einer Studie beeinflussen und zu falschen Schlussfolgerungen führen. Die Erkennung und Berücksichtigung solcher Fehler ist daher essenziell, um die Integrität und Validität einer Studie zu gewährleisten.

Ein bewusster Umgang mit Daten und ein Verständnis für die zugrundeliegenden statistischen Konzepte sind unerlässlich, um valide und verlässliche Ergebnisse zu erzielen und die wissenschaftliche Gemeinschaft sowie die breitere Öffentlichkeit korrekt zu informieren.